Comentario: el sargento McCormitt es muy exigente pero poco preciso en su órdenes. Pedía formar 17 soldados en «5 filas de 4 hombres«. El soldado Smith simplemente multiplicó 5 x 4 = 20 por lo que pensó que el sargento se equivocaba.
McCormitt no dijo que debían ser «5 filas de 4 hombres distintos«. He aquí el truco: basta con colocar 1 soldado que sea común a las 5 filas y se dispondrá de 4 filas de 4 hombres que hacen 16 y el soldado común a todas proporciona los 17 soldados.

Pedro García, nos ha enviado además de la solución anterior que es nuestra favorita, otras tres propuestas muy interesantes. ¡gracias! (^_−)☆

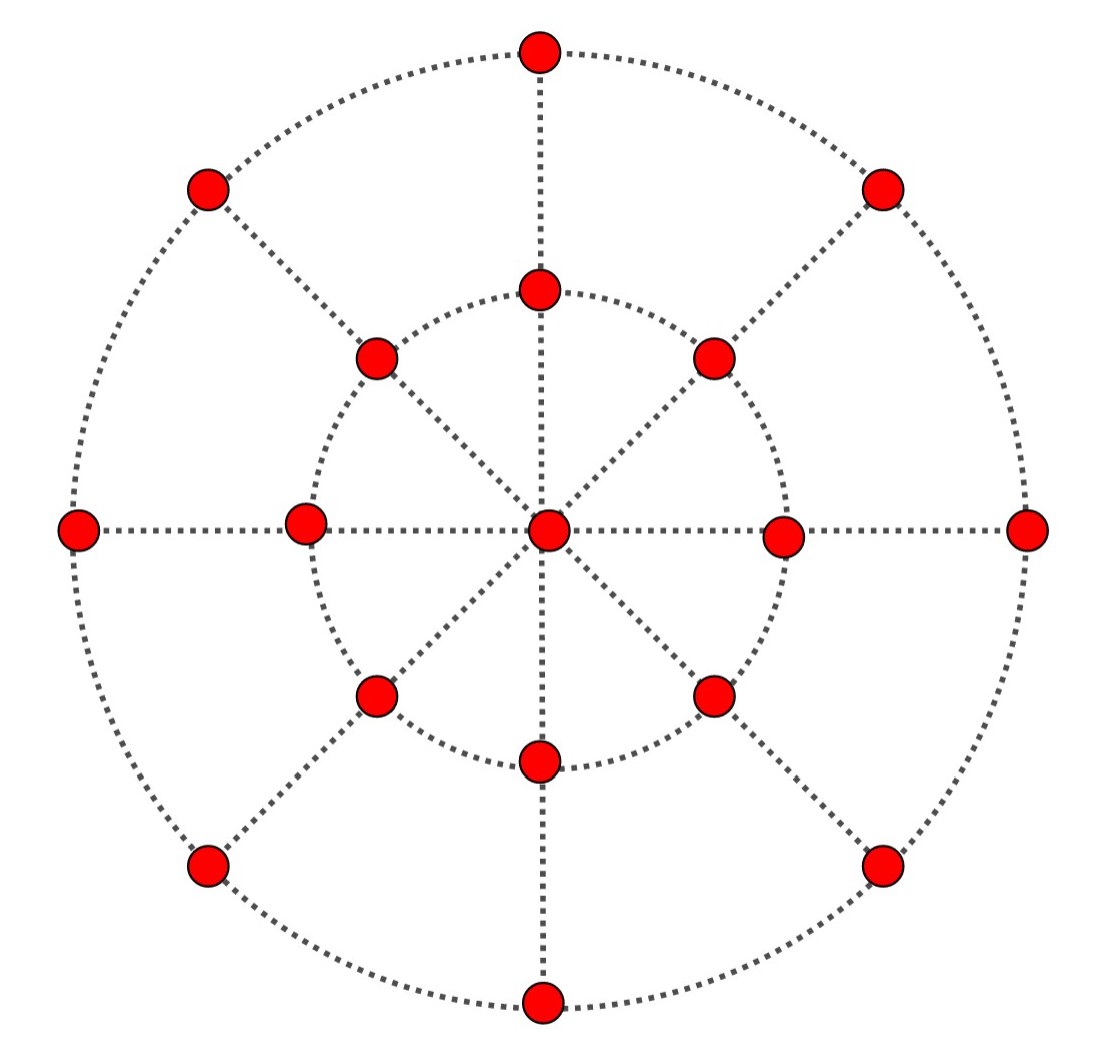
Esta es la que más nos gusta. No caben objeciones por parte de McCormitt. No hay tres soldados alineados así que están formados en cuatro filas de cinco. ¿por qué decimos ésto?
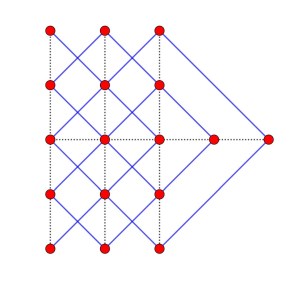
Entre todas las posibilidades hay que tener cuidado en lo que el McCormitt interpreta como fila: si para él fila es un segmento que pasa por tres puntos (dos puntos siempre determinan un único segmento), hay algunas soluciones que no le servirían al sargento.
En las dos últimas configuraciones aparecen varias ternas de puntos alineados que se han dibujado en azul y morado y línea continua, lo que podría hacer que el siempre malhumorado sargento reprendiera al poco afortunado soldado Smith.
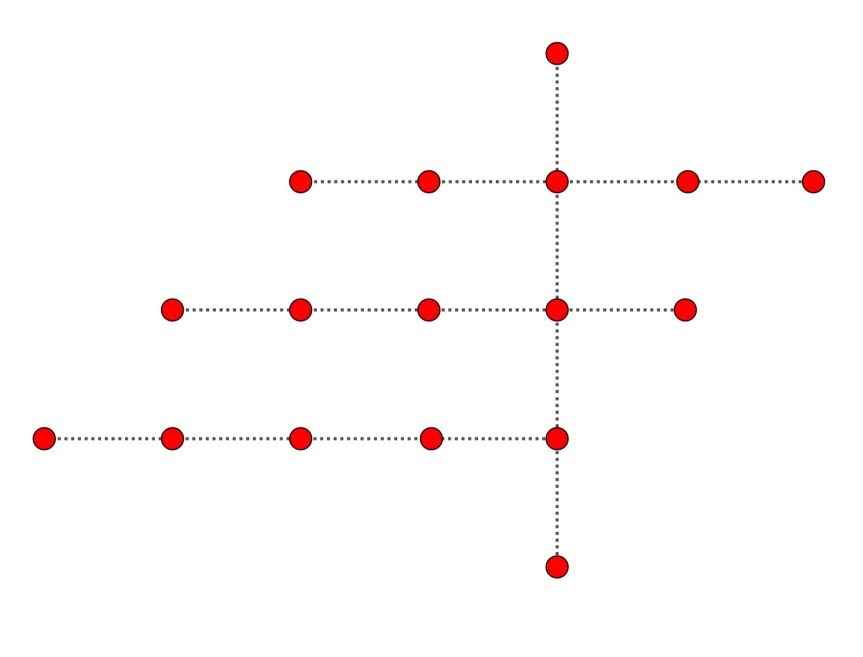
Esta es asimétrica y permite varias configuraciones moviendo la columna vertical a los 4 lugares posibles. Presenta el problema de que el sargento podría decir que hay otras 6 filas extras de tres soldados.
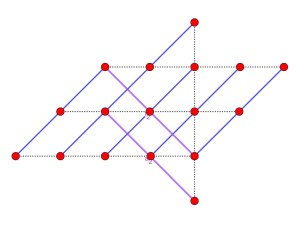
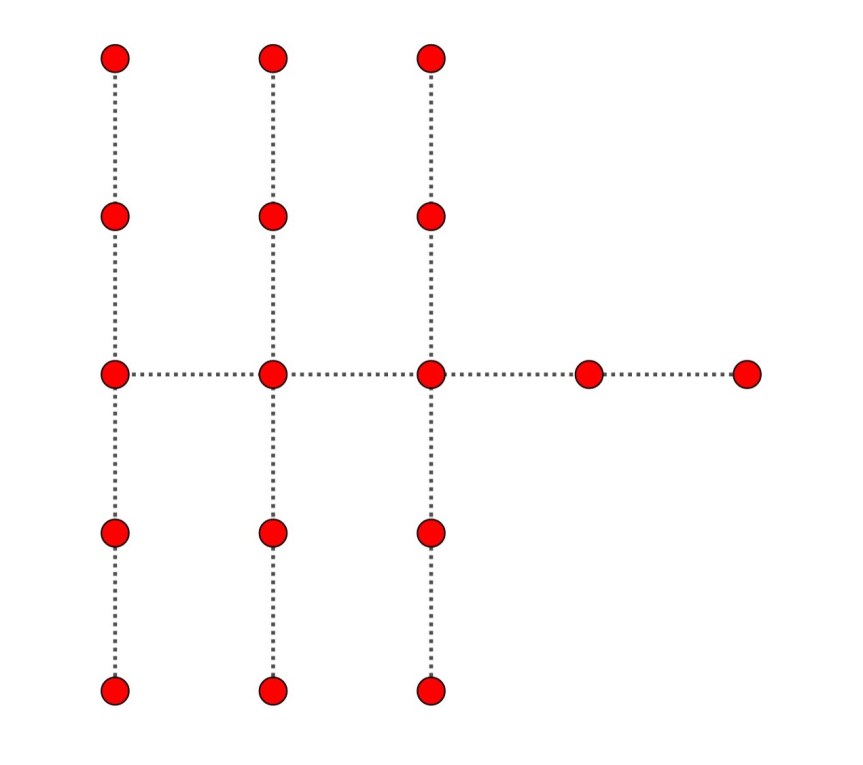
Esta también es asimétrica y también permite varias configuraciones moviendo la fila horizontal a los 4 lugares posibles.
Presenta el problema de que el sargento podría decir que hay otras 6 filas extras de tres soldados.